Простая линейная регрессия на C#

Как уже писал, занимаюсь освоением самых- самых основ machine learning. В курсах и литературе по ML обычно начинают с простой линейной регрессии. Предварительно обучив по массиву значений одной независимой переменной (X) и массиву значений зависимой от ней второй переменной (Y), можно для какого-либо x получить предположительное y. Например, по росту предположить вес.

Код написал на c#. Он находится на гитхабе — ВОТ ТУТ . Это библиотека, в которой на настоящий момент нет ничего, кроме класса простой линейной регрессии 🙂 Для начала объявляем два массива значений с плавающей запятой, равные по длине (для значений x и для значений y). Также объявим ряд переменных для хранения значений стандартного отклонения X, стандартного отклонения Y, пирсоновской корреляции, slope («a», наклон графика в линейном уравнении) и interception («b» — отступ по оси ординат от оси абсцисс). Напомню вид линейного уравнения: y = ax + b.

public double[] xVals, yVals;
public double standardDevX, standardDevY, correlation, slope, interception;

Конструктор класса SimpleLinearRegression будет принимать 2 наших массива (xVals и yVals в коде). При вызове конструктора переменные инициализируются полученными в аргументах  массивами.

this.xVals = xVals;
this.yVals = yVals;

Далее в конструкторе вызывается метод получения стандартного отклонения для массива значений x (xVals) и аналогично для y (yVals). Этот метод, рассмотрим несколько позже.

standardDevX = GetStandardDeviation(xVals);
standardDevY = GetStandardDeviation(yVals);

Далее, опять же в конструкторе, вызываем метод получения пирсоновской корреляции между массивами — его также потом рассмотрим.

correlation = GetCorrelation(xVals, yVals);

Ниже рассчитываем slope (наклон графика). Он будет равен корреляции, умноженной на стандартное отклонение для Y и деленной на стандартное отклонение для X.

slope = correlation * standardDevY / standardDevX;

И последнее в конструкторе — расчет отступа от оси абсцисс по оси ординат (interception). Он будет равен разности среднего значения в массиве значений Y и произведения наклона на среднее в массиве X.

interception = GetArrMean(yVals) - slope * GetArrMean(xVals);

Ниже полный код конструктора:

public SimpleLinearRegression(double[] xVals, double[] yVals)
{
    this.xVals = xVals;
    this.yVals = yVals;
    standardDevX = GetStandardDeviation(xVals);
    standardDevY = GetStandardDeviation(yVals);
    correlation = GetCorrelation(xVals, yVals);
    slope = correlation * standardDevY / standardDevX;
    interception = GetArrMean(yVals) - slope * GetArrMean(xVals);
}

Далее идет метод для получения y по заданному x. Этот метод будет вызываться в приложении, использующем библиотеку. В нем всё просто — принимает в качестве аргумента x, возвращает y.

public double PredictY(double x)
        {
            return interception + slope * x;
        }

Дальше метод для расчета среднего в массиве значений. Не знаю, зачем сделал для этого отдельный метод, ну да ладно 🙂 Метод принимает массив, возвращает среднее…

private static double GetArrMean(double[] arr)
        {
            return arr.Sum() / arr.Length;
        }

Дальше посмотри на метод, используемый в конструкторе класса для получения стандартного отклонения. Он принимает массив значений с плавающей запятой и возвращает стандартное отклонение.

Вначале считаем среднее в массиве (double mean). Далее создаем массив (arrDev) double, такой же по длине, как и принимаемый методом массив (назовем его arr), и заполняем его в цикле значениями. Эти значения рассчитываются как разность значения arr[i] и среднего арифметического для значений всего arr, возведенная в квадрат.

После этого считаем квадратный корень из частного суммы значений массива отклонений arrDev и длины массива arrDev. Если мы имеем дело с выборкой, а не со всей генеральной совокупностью, то из делителя еще вычитаем 1. Полученное значение и возвращает метод. Ниже формула без расчета квадратного корня.

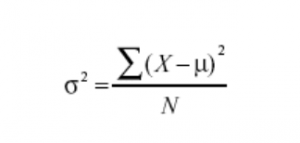
А теперь код метода:

private static double GetStandardDeviation(double[] arr)
        {
            double mean = GetArrMean(arr);
            double[] devs = new double[arr.Length]; //отклонения от среднего
            for (int i = 0; i < arr.Length; i++)
            {
                devs[i] = Math.Pow(arr[i] - mean, 2);
            }
            return Math.Sqrt(devs.Sum() / (devs.Length - 1));
        }

И последний метод — расчет пирсоновской корреляции для двух массивов значений с плавающей запятой. Он принимает 2 массива double в качестве аргументов.

Вначале считаем среднее для каждого массива и создаем 2 массива x и y такой же длины, как и X и Y, принимаемых методом.

double XMean = X.Sum() / X.Length;
double YMean = Y.Sum() / Y.Length;
double[] x = new double[X.Length];
double[] y = new double[Y.Length];

Заполняем массив x значениями — разность X[i] и среднего в массиве Y. Аналогично для y.

for (int i = 0; i < X.Length; i++)
{
     x[i] = X[i] - XMean;
     y[i] = Y[i] - YMean;
}

Теперь создаем еще один массива double для хранения произведений x[i] и y[i]. После этого создаем еще 2 массива для хранения x[i] в квадрате и y[i] в квадрате. Заполняем их:

double[] xy = new double[X.Length];
for (int i = 0; i < X.Length; i++)
{
    xy[i] = x[i] * y[i];
}

double[] xPowed = new double[X.Length];
double[] yPowed = new double[Y.Length];
for (int i = 0; i < X.Length; i++)
{
    xPowed[i] = Math.Pow(x[i], 2);
    yPowed[i] = Math.Pow(y[i], 2);
}

Метод возвращает частное от деления суммы значений массива произведений x и y (массив xy) на квадратный корень из произведения суммы значений массива xPowed (x-ы в квадрате) на сумму значений yPowed). Вот формула для расчета корреляции:

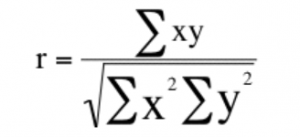
Ниже весь код метода:

private static double GetCorrelation(double[] X, double[] Y)
        {
            double XMean = X.Sum() / X.Length;
            double YMean = Y.Sum() / Y.Length;
            double[] x = new double[X.Length];
            double[] y = new double[Y.Length];

            for (int i = 0; i < X.Length; i++)
            {
                x[i] = X[i] - XMean;
                y[i] = Y[i] - YMean;
            }

            double[] xy = new double[X.Length];
            for (int i = 0; i < X.Length; i++)
            {
                xy[i] = x[i] * y[i];
            }

            double[] xPowed = new double[X.Length];
            double[] yPowed = new double[Y.Length];

            for (int i = 0; i < X.Length; i++)
            {
                xPowed[i] = Math.Pow(x[i], 2);
                yPowed[i] = Math.Pow(y[i], 2);
            }

            return xy.Sum() / Math.Sqrt(xPowed.Sum() * yPowed.Sum());
        }

Использовать библиотеку очень просто. Вначале объявляем и инициализируем значениями с плавающей запятой 2 массива (xVals и yVals). На них машина будет обучаться.

Далее, предварительно добавив ссылку на библиотеку MachineLearningLib, Создаем объект класса SimpleLinearRegression, передав в конструктор наши массивы. Теперь вызываем метод PredictY, передавая ему значение x. Метод возвратит рассчитанный y.

Собственно вот и всё 🙂

Код я писал, опираясь на статьи про линейную регрессию ВОТ ОТСЮДА.

На очереди множественная линейная регрессия, логистическая регрессия и метод ближайших соседей. Авось разберусь 🙂